
The First Personality Reading Based On
The Sacred Geometry Of Your Name Symbols.
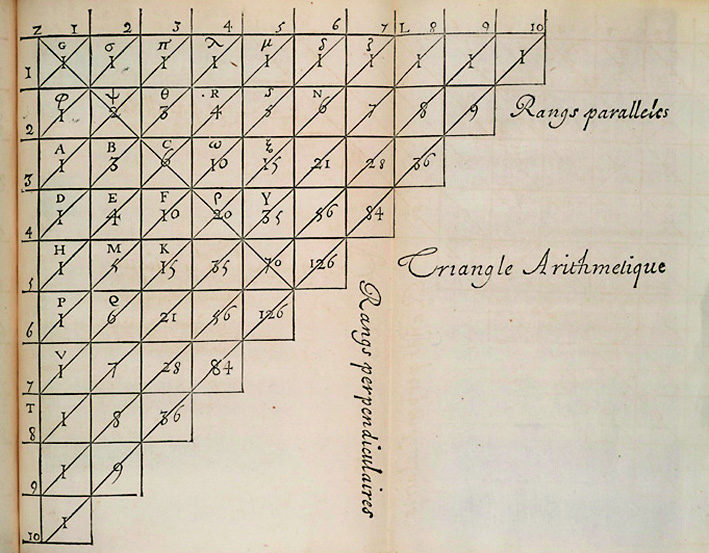

The Pascal's triangle takes its name from the fact that Blaise Pascal was the author of a treatise on the subject, the Traité du Triangle Arithmétique (1654). However, it was already known to Arab mathematicians in the 10th century and its traces can be found in China in the 11th century. It appears in the Jade Mirror of the Four Elements by Zhu Shijie in 1303 (visual opposite).
Pascal's triangle allows the visualization of the binomial coefficients in the form of a triangle.
What is it about? Quite simply to define the number of groups composed of k elements that can be formed in a total set of n elements. They are combinations and not arrangements, the order does not intervene (AB = BA).

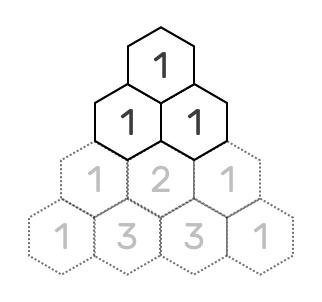
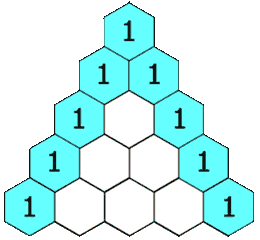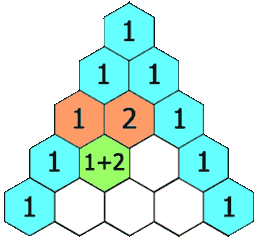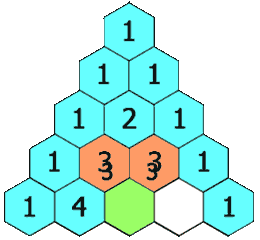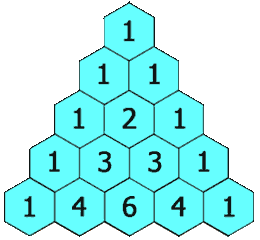

Triangular numbers are obtained by adding integers :
Number one begins all integers sequences, so the "first visible" triangular number is the triangle.
The number 10, fourth triangular number, corresponds to the famous Pythagorean symbol of the Tetraktys.
Triangular numbers mark the first step in combinatorial logic, starting with the enumeration of two-by-two relationships, between two points, two words or two people taken from a group of n elements.
Between two people there is only one possibility to form a "couple", to establish a link. Among three persons, there are 3 links: ab, ac and bc. In a group of four people, the number of combinations is 6: ab, ac, ad, bc, bd and cd.
Tetrahedral numbers are obtained by adding Triangular numbers :

Their name suggests they represent the number of dots needed to make pyramids with triangle bases.
Just as triangular numbers represent the number of binary combinations within a set, tetrahedral numbers correspond to the number of three-element groups that can be formed among a set of n elements.
Between three people there is only one possibility to form a group of 3 (or a triangle). Among four persons, there are 4 possibilities: abc, bcd, cda and dab. In a group of five people, the number of combinations is 10, etc
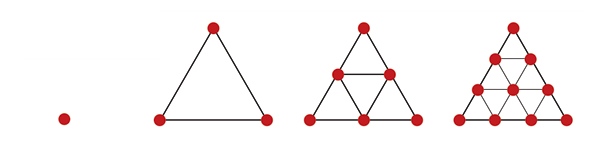
The columns continue in this way, describing the “simplex” which are a generalization of the notion of a triangle or tetrahedron to upper dimensions.
For example,

The first column of the table represents the studied system comprising n elements, from 1, represented by a point, up to 4, represented by a tetrahedron.
The columns represent the k successive elements: nothing, number of points in the figure, number of lines, number of surfaces (triangle), number of volume (tetrahedron).
We can see that in a tetrahedron (yellow hexagons) there are 4 points, 6 lines, 4 triangular faces and finally 1 tetrahedron.
The column ∅ corresponds to the case where no element is taken into account (empty set).
(*) : You will notice that to build a figure in n dimension you need as many n + 1 points or n + 1 figures of dimension n - 1 (called "cell" above):
The fifth line gives us the composition of a 4D triangle, or pentatope, or 5-cell :
Knowing that an n-simplex has n vertices, we can base ourselves on the visualization of the numbers using points which will be used as vertices.
The pentagram and the hexagram are indeed 2D "shadows" or "projections" of triangles respectively of fourth (4D) and fifth dimension (5D).

If we add up the numbers of each row, that is to say all the possible combinations in a set of n elements, we see that the progression forms the series of Powers of 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, etc.
This sequence, whose first four terms are part of the archetypal matrix (numbers 1, 2, 4 and 8) as well as the Plato's Soul of the World, is related to the undulatory phenomena, characteristic of man.
The progression of the powers of 2 corresponds in every way to the ramifications of the family tree as well as to the process of cell division.
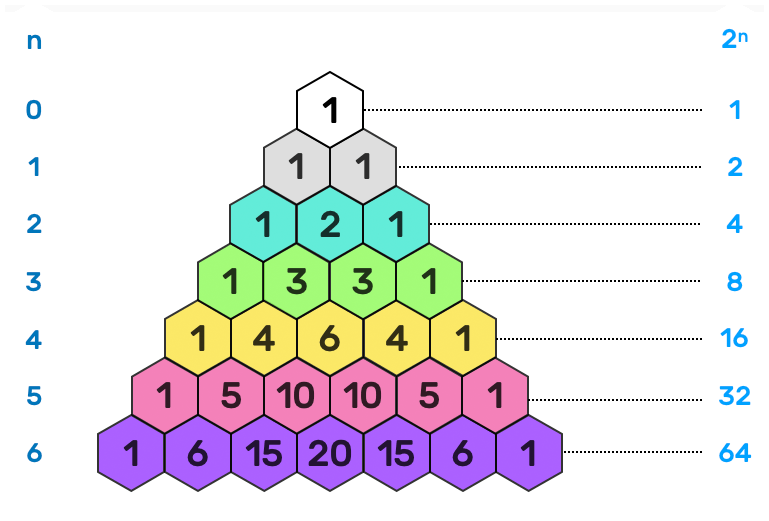
Adding a new element doubles the number of total combinations.
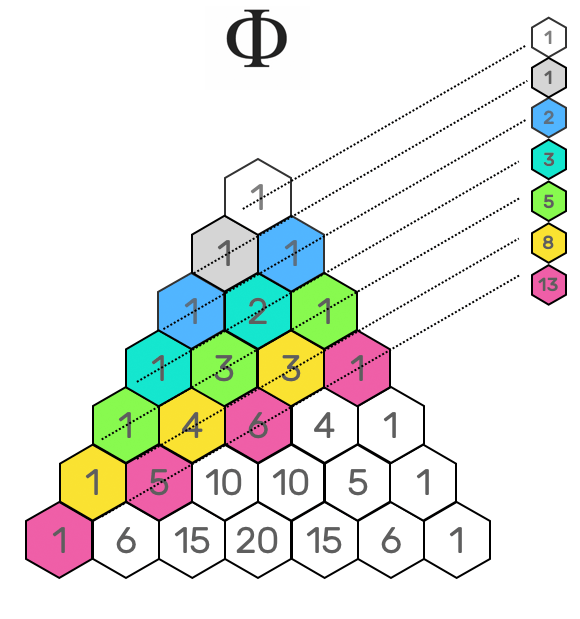
By adding up the values of the same color ... you will get the Fibonacci Sequence, relating to Golden Number: 1, 1, 2, 3, 5, 8, 13, 21, etc
To get the Fibonacci Sequence starts "0, 1" and then continues by adding the two previous numbers :
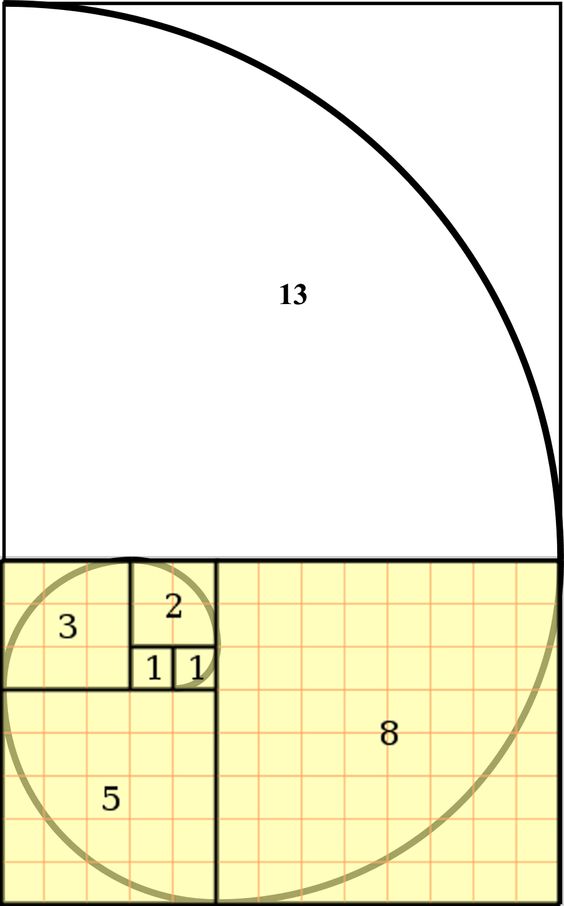
We can qualify these forms as fractals (word invented by the mathematician Benoît Mandelbrot in 1974 on the Latin root fractus "broken", "fractured") because the initial form (triangle or square) persists, only the scale evolves over time.
We can also speak of isometric growth or self-similarity.


By coloring the Odd and Even numbers, you discover the same pattern as the Sierpinski Triangle.
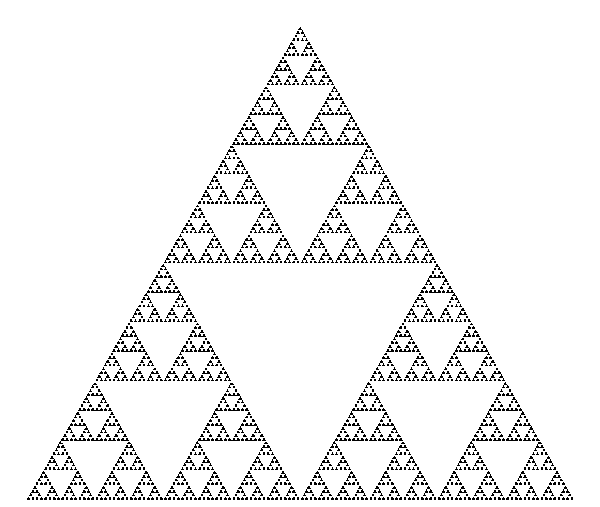
This is a shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles.
